Problem:

Barney's Journey:

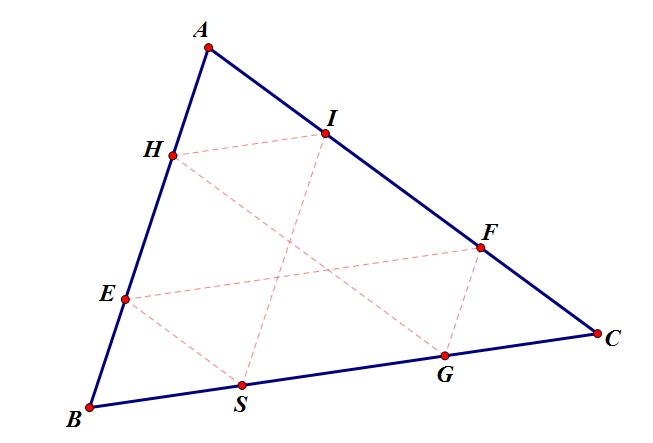
Barney started his journey at point S. He made 5 changes in direction before reaching his starting point which is at point S. During his journey, Barney ran into a wall 5 times before returning to his starting point. If we count the side of the triangular room he started on, which is side BC, Barney will hit each side of the triangular room twice once he reaches his original starting place.

Exploration Questions:

1) Will Barney always return to his starting point?

After some exploration and investigation with Barney's Journey, I have came to the conclusion that no matter which point Barney starts on side BC of triangle ABC, he will return to his starting point S. Interestingly, the amount of direction changes that Barney makes will also stay consistent. Therefore, regardless of his starting point of side BC, he will make 5 direction changes and run into 5 walls before return to his initial starting point S.

(See the GSP images below for my conjectures)

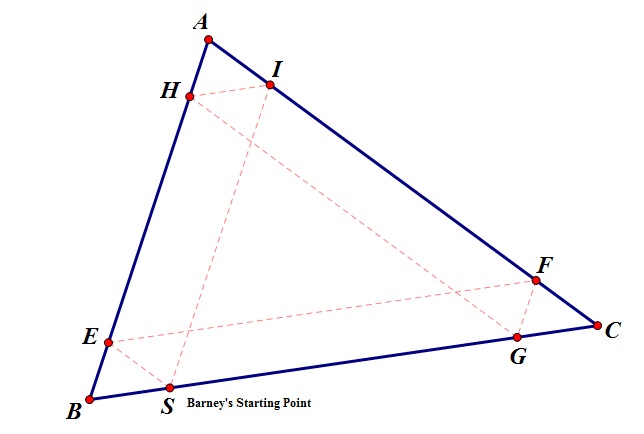
2) If so, will Barney always travel the same distance?

After using the measurement and calculation tools in GSP, I have made a conjecture about the distance that Barney travels on his journey. Regardless of the Barney's initial point S on side BC, he will always travel the same distance before returning to his starting point S. After investigating with this question, I saw that as I moved Barney's starting point S along the side BC, the distances that he traveled before reaching a wall were changing as I moved S, but the total distance traveled was staying consistent.

(Click following link "Bouncing Barney" for exploration and investigation with question 2)

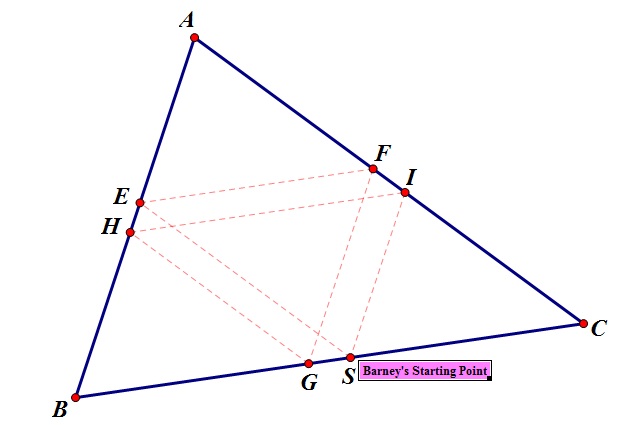
3) Does the path create a pattern of similar triangles?

Barney's path creates four triangles inside the triangular room in which he is bound. Most of the time, three of the four triangles are congruent with the remaining triangle being similar to the other three. Therefore, all of the angles in the four triangles are congruent but the smaller triangle in the middle does not share the congruent side lengths that the other three triangle share. There are two other cases of triangle similarity which depend on Barney's initial position. In one case, Barney's unique starting position creates four congruent triangles. The second case will b discussed in the next question. See GSP image below to see the path that creates 4 congruent triangles:

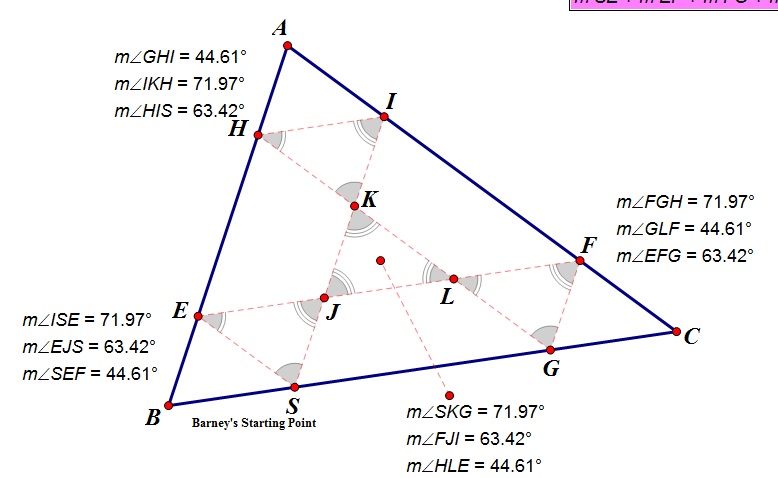
4) Where might his starting point be so that the path would create congruent triangles?

There are two initial starting positions where Barney's path will create congruent triangles. The first starting position can be seen in the GSP image above, where Barney's starting position creates four congruent triangles. In the other case, if Barney's Starting position S lies on a point which is a third of side BC, then three congruent triangles will be created by Barney's path. See GSP image below:

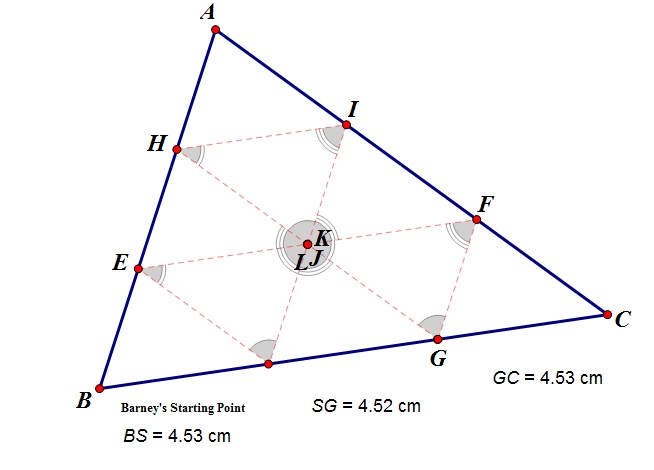
(Click link "Bouncing Barney" to explore question 3 & 4)

5) What if Barney started at a point inside the triangle?

If Barney's starting point is inside the triangle ABC, interestingly enough, everything stays consistent as if he started on the side BC of the triangle. When Barney starts at any point inside the triangle, he will still end up at the same point where he started. Similar to the previous examples, Barney's path will still create similar triangles if he starts inside the triangle ABC. The only difference that I could find was that he will hit one more wall or change direction one more time than in the previous examples. Lets take a look at Barney's path when he starts inside the triangle ABC.

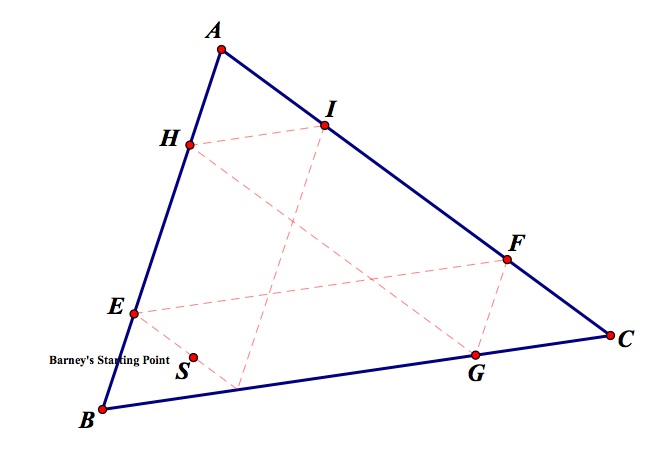
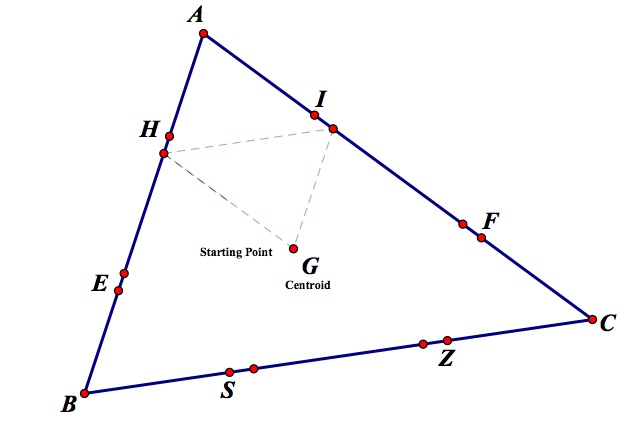
6) What if Barney's starting point was at the centroid? Orthocenter?

The investigation to question 6 was very interesting. If Barney starts at the centroid of the triangle, his path will only make one triangle and return to his starting place after only two change of directions. This logically makes sense because the centroid is the center mass or the balance point of any triangle. (See below Barney's path started at the centroid of ABC)

Now lets observe Barney's path when he starts at the orthocenter of the triangle:

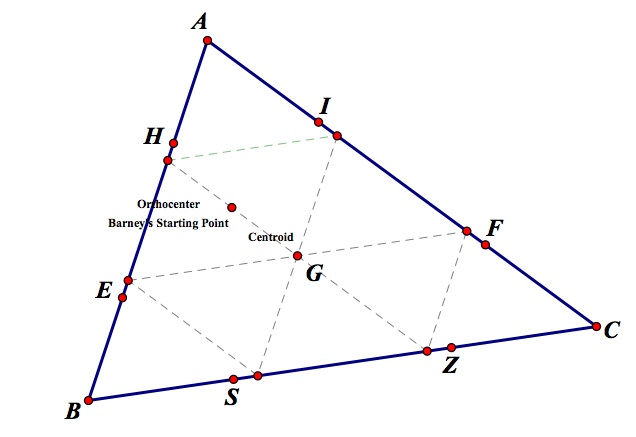
When Barney starts at the orthocenter of the triangle, his path will create three congruent triangles with congruent sides and angles. The path created when Barney starts at the orthocenter is the same path that we discussed earlier when Barney starts on a "third" mark on side BC of triangle ABC. In conclusion, no matter where Barney starts inside the triangle ABC, he will always return to his starting point. Also, Barney's path will always create a certain number of congruent or similar triangles. Regardless of Barney's starting place, his path will create three cases: (1) three congruent triangles with a four triangle which is similar to the three congruent triangles (2) three congruent triangles either by starting at a tick mark which is a third of side BC or starting at the orthocenter of the triangle ABC (3) four congruent triangles, and lastly (4) one triangle for when he starts at the centroid of triangle ABC.